排列问题
问题描述
输入一个字符串,输出去重的全排列(如果有重复的)。这意味着,您必须按所有可能的顺序对输入中的所有字母进行排列。
说明范例
permutations('a'); // ['a']
permutations('ab'); // ['ab', 'ba']
permutations('aabb'); // ['aabb', 'abab', 'abba', 'baab', 'baba', 'bbaa']分析
所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序,本题目相当于全排列。两个元素的全排列$$A_2^2$$=$$2!$$=2,即[i,j]的全排列为[ij,ji]。那么如果是$$A_3^3$$=$$3!$$=6是怎么样的过程,假设有[a,b,c],先选择a作为第一个元素,剩下[b,c]相当于一个$$A_2^2$$,接下来选b作为第一个元素,剩下[a,c]相当于一个$$A_2^2$$,以此类推。
求无重复元素集合的排列数量
假设没有重复元素的情况,等价子问题应当是:对子串中每个元素做首元素的情况,进行其他元素的全排列。因此就有以下的实现:
/**
* idea1 先处理没有重复字母的情况
* 注意:这里为了方便处理,str其实是str.split("")
* 如果str不包含重复字母,数量关系上应该是:permutations(str) = str.length * permutations(str*)
* 理论上递归的终止条件是str.length === 1,此时应当返回1
* @param str
*/
function permutations(str) {
if (str.length === 1) {
return 1;
}
let result = 0;
// 理论上求str组合数,要讨论str每一个元素做起始元素的情况,所以循环str是一定的
for (let i = 0; i < str.length; i++) {
let newArr = [...str];
newArr.splice(i, 1);
result += permutations(newArr);
}
return result;
}其实“每个元素做首元素”的方式有很多,上述代码中通过创建元素组拷贝,从中splice掉作为首元素的元素,剩下的数列进行递归。这个过程或产生临时数组,试图先对这个问题进行一些优化。
不产生临时变量就要求我们在原数组上进行操作,将str[i]提到str[0],原来的str[0]到str[i-1]的元素分别后移,这种情况需要一个临时变量来进行移动。但是实际上我们并不需要str[0]到str[i-1]的元素都移动,因为我们是求全排列,输入的集合顺序并不产生影响。那么我们只需要将str[0]和str[i]进行对换,这时也只需要一个临时变量。
解决了做首元素的问题,那么如何解决对剩余元素进行递归呢?我们不适用临时数组后,递归调用总是使用原数组,那么当前调用总是针对数组的“剩余部分”--str[step]-str[str.length-1],因为str[0]-str[step-1]总是我们已经确定的序列,所以我们做一个标记,来让当前调用知道递归到了什么程度。
因此我们有以下实现:
function swap(str, a, b) {
let temp = str[a];
str[a] = str[b];
str[b] = temp;
}
/**
* idea2 在idea1的前提下,优化临时数组的问题
* @param str
* @param step 标记递归到了哪一步,默认是0
*/
function permutations2(str, step = 0) {
if (str.length === step + 1) {
// console.log(str.join(""))
return 1;
}
let result = 0;
// 本次调用针对是的str[step]到str[str.length-1]的子串
for (let i = step; i < str.length; i++) {
// 对换来得到除了首字母以外的剩余部分
swap(str, step, i );
// 针对剩下的部分
result += permutations2(str, step + 1);
}
return result;
}由于我们还没有解决存在重复字母的问题,permutations2(['a','b','c'])=6,permutations2(['a','b','c','d'])=24,permutations2(['a','b','c','d','e'])=120。看起求全排列的数量似乎并没有问题,但是我们如果在递归结束条件时,输出此时的排列序列,就会发现我们的全排列是有重复的。
我们来一步一步的分析一下。输入str=['a','b','c','d']:
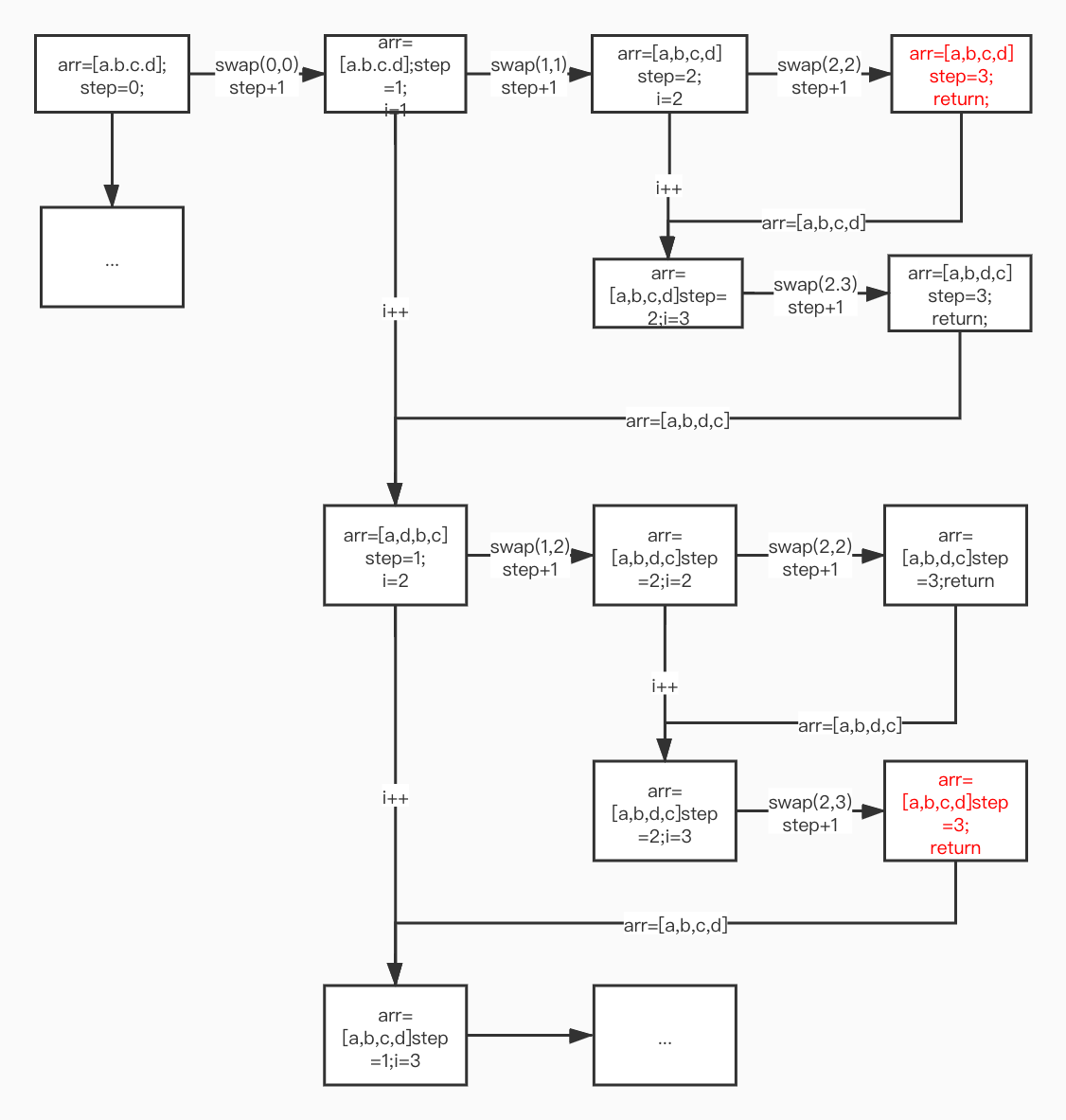
求无重复元素集合的具体排列
其实很容易发现问题,step=1的第一阶段递归,第一轮循环针对的是[b,c,d]这个子序列,而第二轮循环变成了[d,b,c],虽然元素没有变(无序集合中元素是相同的),但是顺序改变了。如果把每次递归针对的子序列看做无序集合,那么排列数是不会错的;如果把每次递归针对的子序列看做是有序集合,那么排序就会有问题。如果不需要输出具体的排列情况,理论上这个算法就没问题,但是如果需要输出具体的排列情况,我们需要把swap这个过程,在递归完成后逆转回来,保证每一轮循环起始的有序集合不发生变化。
每一次递归都会对换一次元素,当递归达到终止条件时,正好得到一个排列,我们将其保存在一个数组中,这个数组随着递归收集所有的结果,最终返回。既能查看所有的排列,数组的长度表达排列数量,于是有了下面的代码:
function swap(str, a, b) {
let temp = str[a];
str[a] = str[b];
str[b] = temp;
}
/**
* idea2 在idea1的前提下,优化临时数组的问题
* @param str
* @param step 标记递归到了哪一步,默认是0
* @param result 保存结果的数组
*/
function permutations2(str, step = 0, result = []) {
if (str.length === step + 1) {
result.push(str.join(""));
return;
}
// 本次调用针对是的str[step]到str[str.length-1]的子串
for (let i = step; i < str.length; i++) {
// 对换来得到除了首字母以外的剩余部分
swap(str, step, i );
// 针对剩下的部分
permutations2(str, step + 1, result);
swap(str, step, i );
}
return result
}求任意集合的具体排列
最后我们来解决存在重复元素的情况。我们假设重复的元素是$$str[m]$$和$$str[n]$$,显然$$m \neq n$$,令$$m<n$$。在这个前提下,我们进行到p阶段,判断swap(p,i)是否在将来会遇到等价的情况,如果遇到则跳过。
当p===i时,原始序列肯定不能跳过;
当p<i时,
如果str[p]===str[i]应当跳过,因为至少是和swap(p,p)是等价的。
如果str[p]!==str[i],则需要从i+1开始寻找q使str[q]===str[i],如果有则跳过。
那么可以得到以下判断函数:
function isEqual(arr, step, i) {
// 自我对换不处理
if (step === i) {
return false
}
// 至少和str[step]的自我对换是等价的
if (arr[step] === arr[i]) {
return true;
}
// 从i+1开始寻找,如果有和str[i],则把交换过程放到swap(step,k)
for (let k = i + 1; k < arr.length; k++) {
if (arr[k] === arr[i]) {
return true;
}
}
return false;
}除了这种判断方式,在众多的代码中还可以看到这样的判断方式:
function isEqual2(arr, step, i) {
for (let p = step; p < i; p++) {
if (arr[p] === arr[i]) {
return true;
}
}
return false;
}核心是从step遍历到i-1,看看是否存在和str[i]相同的元素。step和i相等时,无法构成循环,所以始终为不相同;step和i不相同时,在step到i-1的范围内查找是否有与str[i]相同的元素,有的话就认为这个对换已经被使用过了。其实swap(step,i)的根本含义是用str[i]做step阶段子序列新的首元素,那么只用判断str[i]是否已经在当前子序列靠前的位置中出现过。
对比来看,isEqual考量的是str[i]如果还有机会当首元素,就等下一次机会吧。当step和i相等时,后面有重复的元素,导致认为还有机会,实际上自对换只有一次。如果step和i不相等,str[step]和str[i]相等,但之后并没有重复的元素,所以认为这样的对换之后不会发生,之后是不会发生,但是其本身就是无效对换。因此我们补充了这两种特殊情况完成判断。
总结
排列问题应该是算法的基础题,很容易发现重复子问题,但是去重的思想有多种,且要考虑的情况比较多,也就有了复杂的判断isEqual和简单一些的判断isEqual2。求排列数是一道典型的递归型算法,使用递归就要想好递归的终止条件,且这个问题能够分切成等价的一个个子问题(求子序列的全排列数)。本文从求排列数开始,到求排列结果,到求去重的排列结果,每一步我都有我的理解方式,也许笨重,也许绕了弯子,但是既然掌握的不扎实,就从最笨的方法一点点掌握,希望我能慢慢熟练掌握这样的思考。